Blog:

RM Robotic Arm Singularity Analysis and Avoidance Methods

I. Overview of Singularities

When we use robotic arms, we often encounter singularities (or singularity areas), which cause abnormal movement trajectories of the robotic arms and even make the joint speeds uncontrollable. If we want the robotic arms to successfully complete their tasks, we must understand how singularities (or singularity areas) are generated and how to avoid their impacts.

What Is A Singularity

 Due to the limitation of mechanical limits or soft limits, for most six-axis robotic arms, there might be any case with no inverse kinematic solution in their motion spaces, that is to say, the planned motion of a robotic arm based on coordinates cannot be clearly reversed into the rotation angles of its joint axes. Such a point with no inverse kinematic solution in a robotic arm’s work space is called a "singularity". Mathematically, it means that the Jacobian is not a full rank matrix. Therefore, the Jacobian can be used to determine whether a robotic arm is in a singular state. A singularity is a specific point in a robotic arm’s workspace that causes the robotic arm to lose one or more degrees of freedom (DoF). When a robotic arm’s tool center point (TCP) moves into or near a singularity, the robotic arm will stop moving or move in unexpected manner.

Types of Singularities

Singularities can be classified into four types, namely shoulder, elbow, wrist, and boundary.

The Simple Way to Spot a Singularity

In general, singularities are easy to spot. A robotic arm is moving at a constant and smooth speed along a trajectory … and then it does something “weird.” Its movement changes unexpectedly, and it’s not clear why. Here are a few markers that suggest a robotic arm might have entered or passed near a singularity:

1. It makes a jerky movement or stops suddenly.
2. When it passes near its tool center point (TCP), it entirely slows down or even stops. At the same time, some of its joints suddenly accelerate to their maximum speed. This inconsistency between the overall speed and the speeds of some joints may mean that the robotic arm has entered or passes near a singularity area.
3. It shakes abnormally.

Jacobian Matrix

The Jacobian J is a matrix that describes the relationship between the end effector speeds and the joint speeds of a robotic arm. For a 6 DoF robotic arm, the Jacobian is usually a 6×6 matrix expressed as follows:

where x, y, z indicate the position of the end effector, α, β, γ indicate the attitude angle of the end effector, and q1, q2, ..., q6 are the angles of the joints. The Jacobian can be used in the following calculations:

1. It can be used to convert between the angular velocities of a robotic arm’s joints and the velocity of its end effector.
2. It can be used to convert polar or spherical coordinates into Cartesian coordinates.
3. It can be used to determine if a robotic arm has singularities and where those singularities are in the robotic arm’s workspace.

When a robotic arm enters a singularity, the determinant of the Jacobian for the current configuration becomes zero, which means that there is no solution to the linear equations that are represented by the matrix. In other words, a Jacobian with a determinant of zero has no solution and the robotic arm is at a singularity.

II. Three Basic Types of Singularities

Shoulder Singularities

A shoulder singularity occurs when the center of a robotic arm’s wrist aligns with the axis of Joint 1, or when the axis of Joint 6 becomes coincident with the axis of Joint 1.

Taking RM65 as an example, a shoulder singularity occurs when the center C of its wrist (the intersection of the axes of Joints 5 and 6) is collinear with Axis 1, and the indication point is [0, 43.4, -105.7, 0, -30, 0], as shown in the figure below:

Such singularities will impose 3 unfavorable impacts:

1. Joint 1 has an infinite number of solutions. No matter how Joint 1 rotates, it will not cause a change in the end position. As a result, Joint 1 has an infinite number of solutions.
2. The end loses the ability to move in the y direction. When Joints 2 and 3 rotate, only speeds along the x-axis and the z-axis can be generated, but no speed along the y-axis is generated.
3. Small movements of the end pose require drastic rotation of the joint angle. Due to the instability of the values when performing inverse kinematic calculations, the algorithm may try to make Joints 1 and 4 spin 180° at infinite speed.

Position Jacobian: Assuming that Joint 1 of the robotic arm is collinear with the rotation center of the end effector, the movement of Joints 5 and 6 will not affect the position Jacobian. The position Jacobian will be degraded.

Attitude Jacobian: Since the axes of Joints 5 and 6 coincide with the axis of Joint 1, the attitude Jacobian will also degrade, that is to say, the influence of Joints 5 and 6 on the attitude cannot be distinguished.

When we consider the DH parameters of RM65B and use MATLAB to analyze the singularity, the results are as follows:

It can be seen that although the absolute value of the determinant is large, we are more concerned about the singular values. The minimum singular value is 0.0002, which is basically close to 0. So it can be concluded that the robotic arm is in a singular state at this point.

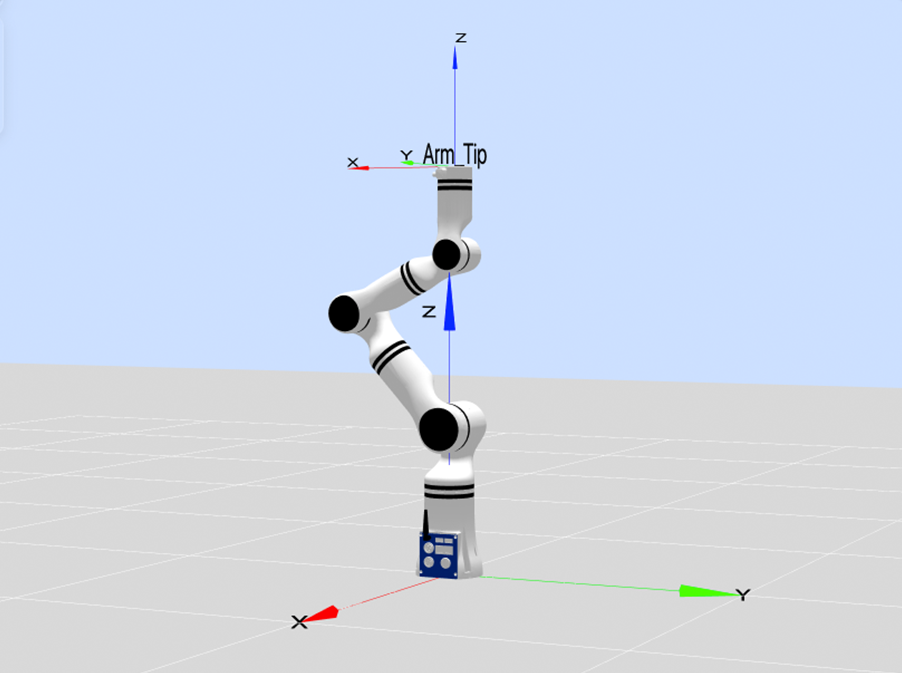
A special case is when Joints 1 and 6 are coaxial and C is collinear with Axis 1, and the indication point is [0, 43.4, -105.7, 0, 62.3, 0], as shown in the figure below:

Elbow Singularities

An elbow singularity can be easily recognized because it looks like the robotic arm has "stretched too far". It occurs when the elbow joint (Joint 3) is at 0°, though this depends on how the home position of the robotic arm is defined. Elbow singularities occur when the center of the robotic arm’s wrist (i.e. the point at which all 3 wrist axes converge) lies on the same plane as Joints 2 and 3.

For example, when q3 = 0, which means the format of point position is [x, x, 0, x, x, x], the indication point is [-90, 60, 0, 0, 90, 0], as shown in the figure below:

When MATLAB is used to analyze, the results are as follows:

It can be seen that although the absolute value of the determinant is large, we are more concerned with the singular values. The minimum singular value is 0.6983, which is close to zero but not very close, which means that the Jacobian is close to being singular but not completely singular. A small singular value indicates that the movement of the robotic arm in certain directions may become unstable, or will significantly slow down.

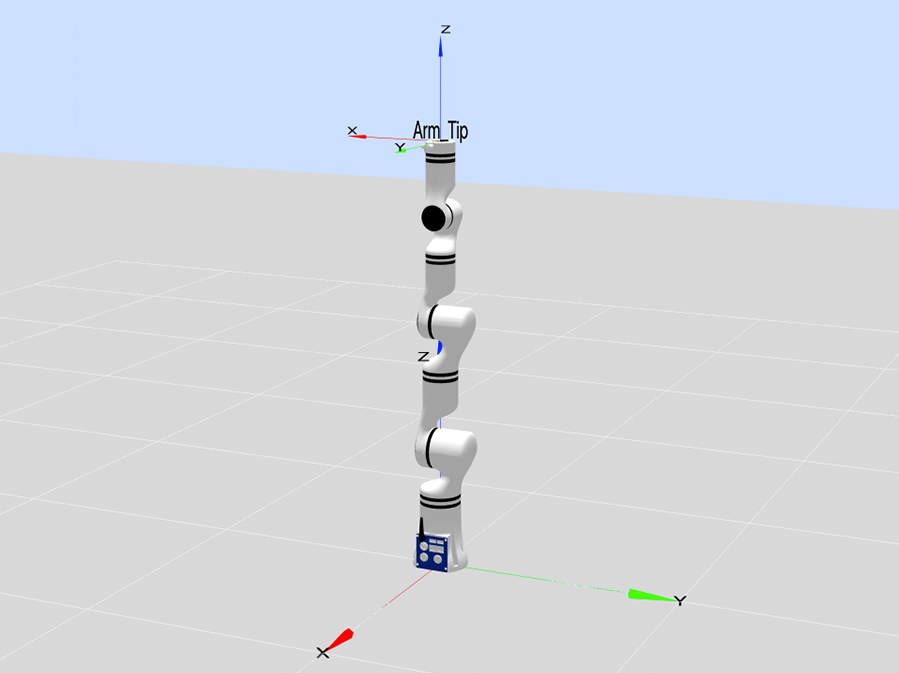
A special case is when Joints 1 and 4 are coaxial and q3 = 0 where an elbow singularity will also occur, which means the format of point position is [x, 0, 0, x, x, x], and the indication point is [0, 0, 0, 90, -60, 0], as shown in the figure below:

Another special case is when Joints 1, 4, and 6 are coaxial and q3 = 0, which means the format of point position is [x, 0, 0, x, 0, x], and the indication point is [0, 0, 0, 90, 0, 0], as shown in the figure below:

Wrist Singularities

A wrist singularity will occur when Joints 4 and 6 are coaxial and q5 = 0, which means the format of point position is [x, x, x, x, 0, x], and the indication point is [0, 60, 30, 0, 0, 0], as shown in the figure below:

When MATLAB is used to verify the results, the results are as shown in the figure below:

The determinant is −1.1578×10−9, which is very close to zero, indicating that the Jacobian loses rank in some directions. The minimum singular value is 0.00000, indicating that the system has completely lost its freedom of movement in some directions. In this case, the robotic arm is completely in a singular state.

Boundary Singularities

There is another type of singularity that occurs at the boundary of a robotic arm's workspace. Whenever a robotic arm’s TCP gets close to a boundary, there is a risk it could enter a singularity. Elbow singularity is an example of workspace boundary singularities.

A special case is when the end of the robotic arm reaches the farthest position and q3 = 0, which means the format of point position is [x, x, 0, x, 0, x], and the indication points are [0, 0, 0, 0, 0, 0], [-90, 90, 0, 0, 0, 0], and [-90, 45, 0, 0, 0, 0], as shown in the figure below.

When the indication point is [0, 0, 0, 0, 0, 0], the MATLAB operation results are as follows:

It can be seen that the determinant of the Jacobian is 0, the minimum singular value is 0, and the robotic arm is in a singular state.

The following indication points [-90, 90, 0, 0, 0, 0] and [-90, 45, 0, 0, 0, 0] are analyzed in the same way.

III. Ways to Avoid Singularities

There are mainly two ways to avoid singularities of robotic arms. The first one is to avoid the robotic arm passing through singularities as much as possible in path planning. The second one is to use the pseudo-inverse of the Jacobian to ensure the stability of the inverse kinematics algorithm near singularities.

For the first way, it is also necessary to avoid the areas near singularities while avoiding the robotic arm passing through singularities. Because all points in these areas will result in numerical instability. The second way is mathematically simpler and more universal, but requires compromising the motion accuracy of the end of the robotic arm to ensure that the robotic arm can pass through the singularity areas.

In practical applications, we need to choose the appropriate way according to work needs. For example, for the task of grabbing objects, even if there is any singularity area at any path point, we don't care how and with what accuracy the end of the robotic arm moves to the target point, but just need it to pass through the singularity areas smoothly. In this case, we can choose the second way. For welding tasks, if the welding point happens to be on the path of the robotic arm's movement, a compromise of accuracy will inevitably affect the welding effect. In this case, it is better for us to choose the first way. We can identify areas where the end path is a singularity and place the welding plate on the path point with no singularity to avoid the robotic arm passing through the singularity areas.