SDK开发指南:
手眼标定 概述
手眼标定通常用于机器人和计算机视觉领域,特别是在需要精确控制机械臂与环境交互的场景中去,手眼标定是将机械臂的末端执行工具(二指夹爪等)和摄像机的坐标系统一起来,解决相机与机械手之间的坐标转换关系,让机械手能精确抓取到相机定位的目标。
手眼系统,是手(机械臂)和眼(相机)的关系,当眼(相机)看到一个物体的时候,需要告诉手(机械臂)物体的位置在哪里,物体在眼(相机)的位置确定了,如果此时有了眼(相机)和手(机械臂)的关系,我们就能得到物体在手(机械臂)的位置了。
当需要进行机器人抓取物体、动态环境交互、精密测量与检测、视觉伺服控制等多个场景时,都需要进行手眼标定。
手眼标定之后,除非相机和机械臂的相对位置发生变动,则不需要重新标定。下面的标定方法适用于正装、侧装和倒装。
手眼标定有两种情况:
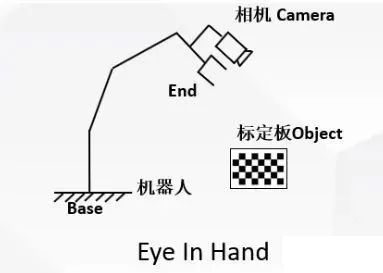
- 一种是相机固定在机械臂上
Eye-in-Hand系统:相机安装在机械臂末端,在机械臂移动过程中随着机械臂一起运动。
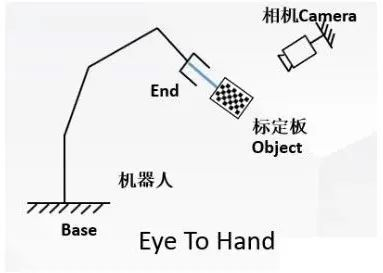
- 第二种是相机固定在机械臂之外某处
Eye-to-hand系统:相机固定在机械臂之外
原理
1.眼在手上(eye-in-hand)
对于eye-in-hand情况,机器人手眼标定即标定得到相机和机械臂末端之间的坐标变换关系:

对目标点的空间三维坐标进行变换的过程中,首先遇到的问题就是机械臂末端坐标系与相机坐标系之间的位置变换关系,也就是机械臂的手眼位置关系,也是手眼标定最后计算的结果,该关系用符号X表示,可以用方程AX=XB求解。其中A表示相邻两次运动时机械臂末端的变换关系;B表示相邻两次运动时相机坐标的相对运动。
如图所示,为眼在手上,也即eye-in-hand。(此处仅是为了演示效果图,而非真实的实验场景)。相机固定在机械臂末端,会随着机械臂的运动而运动。
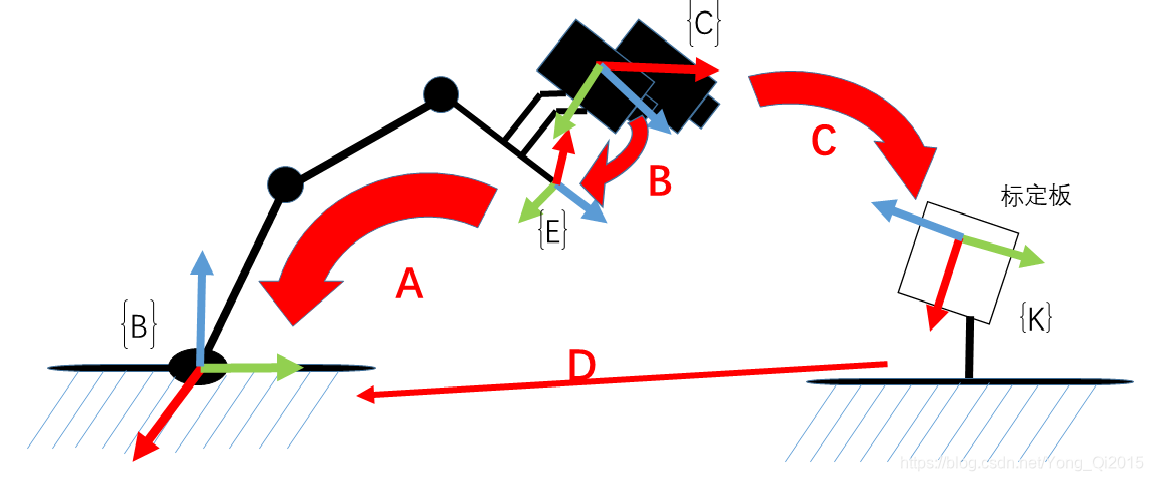
A:机械臂末端在机械臂坐标系下的位姿,通过机械臂API获取。(已知)。
B:相机在机器人末端坐标系下的位姿,这个变换是固定的,只要知道这个变换,我们就可以随时计算相机的实际位置,所以这就是我们想求的东西。(未知,待求)
C:相机在标定板坐标系下的位姿,这个其实就是求解相机的外参(由相机标定求出)。
D:标定板在机器人基坐标系下的位姿。在标定过程中,只有机械臂末端在动,标定板和机械臂基座保持不动,这个位姿关系是固定不变的。
所以我们只要计算得到B变换,那么标定板在机械臂坐标系下的位姿D也就自然得到了
如图所示,我们让机械臂运动两个位置,保证这两个位置下都可以看到标定板,然后构建空间变换回路:
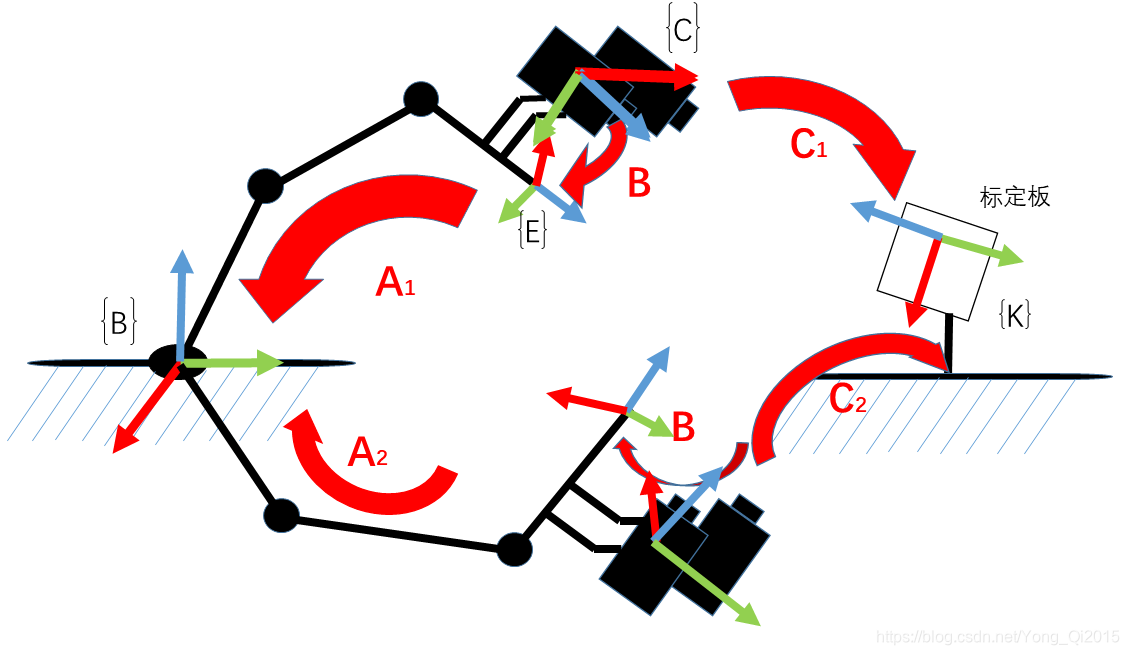
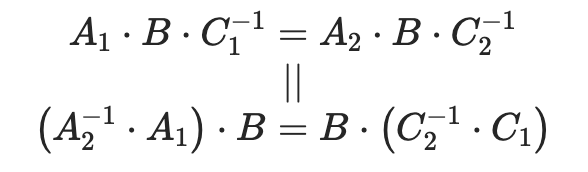
等同于下面的公式:
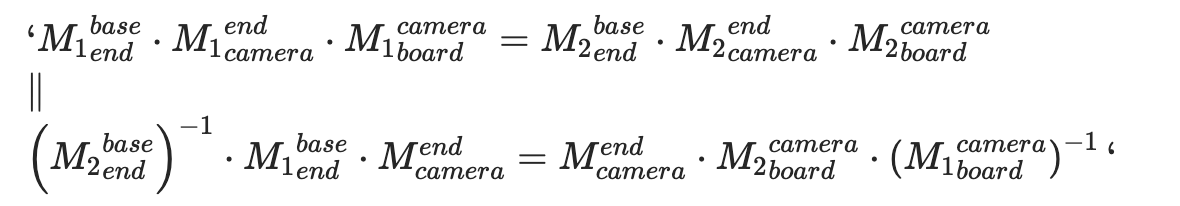
这是一个典型的AX=XB问题,而且根据定义,其中X是一个4X4齐次变换矩阵:
手眼标定的目的就是为了计算出X
2.眼在手外(eye-to-hand)

眼在手外标定时固定机械臂基座和相机,将标定板固定在机械臂末端,所以标定过程中标定板与机械臂末端的关系固定不变,以及相机与机器人基座标的关系固定不变
标定的目标:
相机到机械臂基座坐标系的变换矩阵
实现方法:
- 把标定板固定在机械臂末端
- 移动机械臂末端,使用相机拍摄不同机械臂姿态下的标定板图片n张 (10~20)
每次采集图片和机械臂位姿,都存在下面等式:
其中:
- 标定板到机械臂末端的变换矩阵(因为标定过程中标定板固定在机械臂末端,标定板到机械臂末端的变化矩阵不变)
- 可以通过机械臂末端位姿算出
- 手眼标定需要求的
- 通过相机标定方法得到
则可以得到如下等式:

这也是是一个典型的AX=XB问题,而且根据定义,其中X是一个4X4齐次变换矩阵,其中R是相机到机械臂基坐标系的旋转矩阵,t是相机到机械臂基坐标系的平移向量:
手眼标定的目的就是为了计算出X。
关键代码解释
代码获取
代码可以在github链接获取最新代码。
代码结构
├── eye_hand_data # 眼在手上标定时采集的数据
├── libs
│ ├── auxiliary.py # 程序用到的一些辅助的包
│ └── log_settings.py # 日志包
├── robotic_arm_package # 机械臂python包
├── collect_data.py # 手眼标定时采集数据程序
├── compute_in_hand.py # 眼在手上标定计算程序
├── compute_to_hand.py # 眼在手外标定计算程序
├── requirements.txt # 环境依赖文件
├── save_poses.py # 计算依赖文件
└── save_poses2.py # 计算依赖文件compute_in_hand.py | compute_to_hand.py关键代码解释
1.主函数func()
compute_in_hand.py | compute_to_hand.py
def func():
path = os.path.dirname(__file__)
# 亚像素角点查找准则
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)
# 准备标定板的3D点坐标
objp = np.zeros((XX * YY, 3), np.float32)
objp[:, :2] = np.mgrid[0:XX, 0:YY].T.reshape(-1, 2)
objp = L * objp
obj_points = [] # 存储3D点
img_points = [] # 存储2D点
images_num = [f for f in os.listdir(images_path) if f.endswith('.jpg')]
for i in range(1, len(images_num) + 1):
image_file = os.path.join(images_path, f"{i}.jpg")
if os.path.exists(image_file):
logger_.info(f'读 {image_file}')
img = cv2.imread(image_file)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
size = gray.shape[::-1]
ret, corners = cv2.findChessboardCorners(gray, (XX, YY), None)
if ret:
obj_points.append(objp)
corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)
if [corners2]:
img_points.append(corners2)
else:
img_points.append(corners)上面代码遍历采集的标定板图像,逐一获取棋盘格角点并放到数组中去。
2.相机标定
compute_in_hand.py | compute_to_hand.py
# 标定,得到图案在相机坐标系下的位姿
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)- 使用OpenCV的
calibrateCamera函数进行相机标定,计算相机的内参数和畸变系数。 rvecs和tvecs分别是每张图像的旋转向量和平移向量,表示标定板在相机坐标系下的位姿。
3.处理机械臂位姿数据
compute_in_hand.py
poses_main(file_path)将机械臂末端位姿数据转化为机械臂末端坐标系相对于基坐标系的旋转矩阵和平移向量。
compute_to_hand.py
poses2_main(file_path)将机械臂末端位姿数据转化为基坐标系相对于机械臂末端坐标系的旋转矩阵和平移向量。
4.手眼标定计算
R, t = cv2.calibrateHandEye(R_tool, t_tool, rvecs, tvecs, cv2.CALIB_HAND_EYE_TSAI)
return R,t使用OpenCV的
calibrateHandEye函数进行手眼标定。- 在compute_in_hand.py中计算相机相对于机械臂末端的旋转矩阵 R_cam2end和平移向量 T_cam2end。
Cvoid cv::calibrateHandEye(InputArrayOfArrays R_end2base, InputArrayOfArrays T_end2base, InputArrayOfArrays R_board2cam, InputArrayOfArrays T_board2cam, OutputArray R_cam2end, OutputArray T_cam2end, HandEyeCalibrationMethod method = CALIB_HAND_EYE_TSAI)- 在compute_to_hand.py中计算相机相对于机械臂基座的旋转矩阵 R_cam2base 和平移向量T_cam2base。
Cvoid cv::calibrateHandEye(InputArrayOfArrays R_base2end InputArrayOfArrays T_base2end InputArrayOfArrays R_board2cam InputArrayOfArrays T_board2cam OutputArray R_cam2base OutputArray T_cam2base HandEyeCalibrationMethod method = CALIB_HAND_EYE_TSAI)采用了
CALIB_HAND_EYE_TSAI方法,这是常用的手眼标定算法。
save_poses.py 关键代码解释
1. 定义欧拉角转换为旋转矩阵的函数
def euler_angles_to_rotation_matrix(rx, ry, rz):
# 计算旋转矩阵
Rx = np.array([[1, 0, 0],
[0, np.cos(rx), -np.sin(rx)],
[0, np.sin(rx), np.cos(rx)]])
Ry = np.array([[np.cos(ry), 0, np.sin(ry)],
[0, 1, 0],
[-np.sin(ry), 0, np.cos(ry)]])
Rz = np.array([[np.cos(rz), -np.sin(rz), 0],
[np.sin(rz), np.cos(rz), 0],
[0, 0, 1]])
R = Rz @ Ry @ Rx
return R- 定义了将欧拉角(绕X、Y、Z轴的旋转)转换为旋转矩阵的函数。
- 按照Z-Y-X的顺序进行旋转,并将各轴的旋转矩阵相乘得到最终的旋转矩阵
R。
2. 将位姿转换为齐次变换矩阵
def pose_to_homogeneous_matrix(pose):
x, y, z, rx, ry, rz = pose
R = euler_angles_to_rotation_matrix(rx, ry, rz)
t = np.array([x, y, z]).reshape(3, 1)
H = np.eye(4)
H[:3, :3] = R
H[:3, 3] = t[:, 0]
return H- 将位姿(位置和姿态)转换为4x4的齐次变换矩阵,以便进行矩阵运算。
- 位置
(x, y, z)作为平移向量,姿态(rx, ry, rz)作为旋转欧拉角。 - 生成的齐次变换矩阵
H将用于描述机械臂末端相对于基座的旋转变换。
3. 保存多个矩阵到CSV文件
Copy codedef save_matrices_to_csv(matrices, file_name):
rows, cols = matrices[0].shape
num_matrices = len(matrices)
combined_matrix = np.zeros((rows, cols * num_matrices))
for i, matrix in enumerate(matrices):
combined_matrix[:, i * cols: (i + 1) * cols] = matrix
with open(file_name, 'w', newline='') as csvfile:
csv_writer = csv.writer(csvfile)
for row in combined_matrix:
csv_writer.writerow(row)将多个矩阵横向拼接成一个大矩阵,然后保存到CSV文件中。
每个矩阵占用固定的列数,这样在读取时可以按照固定的间隔切分出单个矩阵。
标定过程
1.环境要求
基础环境准备
| 项目 | 版本 |
|---|---|
| 操作系统 | ubuntu/windows |
| Python | 3.8 及以上 |
Python环境准备
| 包 | 版本 |
|---|---|
| numpy | 2.0.2 |
| opencv-python | 4.10.0.84 |
| pyrealsense2 | 2.55.1.6486 |
| scipy | 1.13.1 |
执行下面命令在python环境中安装手眼标定程序所需要的包:
pip install -r requirements.txt设备准备
机械臂:RM75 RM65 RM63 GEN72
相机: Intel RealSense Depth Camera D435
摄像头专用数据线
网线
标定板(1或2都可以)
- 打印纸质标定板。

- 淘宝上搜索“标定板棋盘格”购买。
- 打印纸质标定板。
程序里的API版本和机械臂控制器版本对应
程序里的的机械臂API版本为4.3.3。
打开示教器,查看当前机械臂控制器版本。
示教器:配置-机械臂配置-版本信息。

查看机械臂控制器版本和当前程序使用的机械臂API版本是否对应,详细版本对应关系,请参考版本变更说明。
根据控制器版本和API版本对应关系,选择特定版本的控制器软件或者机械臂API进行升级替换。
- 升级控制器版本方法web版示教器使用说明。
2.标定过程
参数配置
在配置文件(config.yaml)中设置标定板参数和机械臂类型。
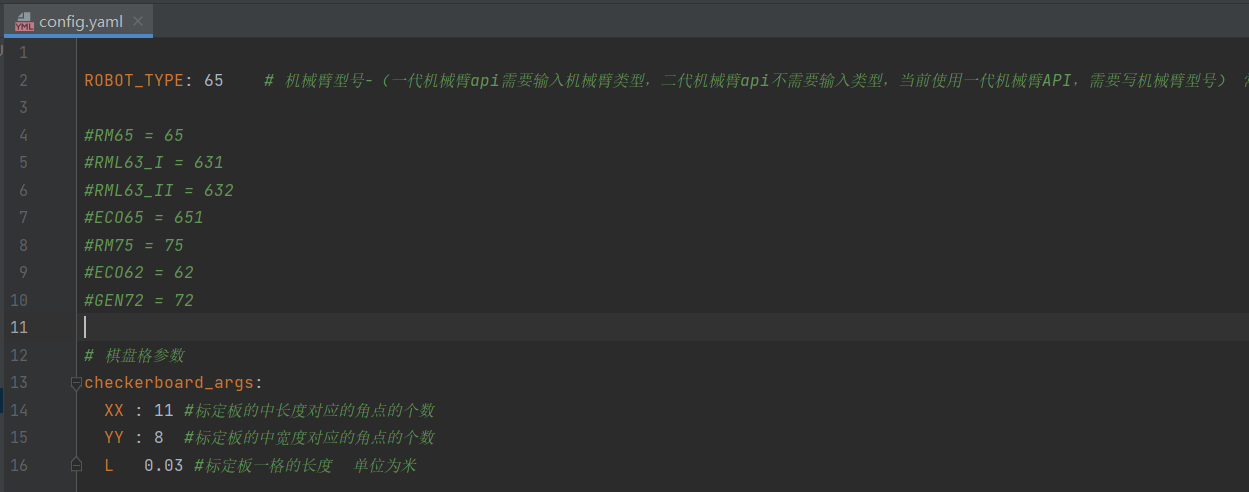
config.yaml里的配置文件如下,有下面四个:
- ROBOT_TYPE:机械臂型号,默认是65 ,对应RM65臂。
- xx:标定板的横向角点数(长边格子数减1),默认为11,例如下图长边12个格子,角点数为11。
- YY:标定板纵向角点数(短边格子数减1),默认为8,例如下图短边9个格子,角点数为8。
- L : 标定板单个方格的实际尺寸(单位:米),默认是0.03。

眼在手上
采集数据
- 相机连接线连接电脑和D435相机,网线连接电脑和机械臂。
- 电脑的ip和机械臂设置为同一网段。
- 如果机械臂IP为192.168.1.18 ,则将电脑 ip地址设为1网段。
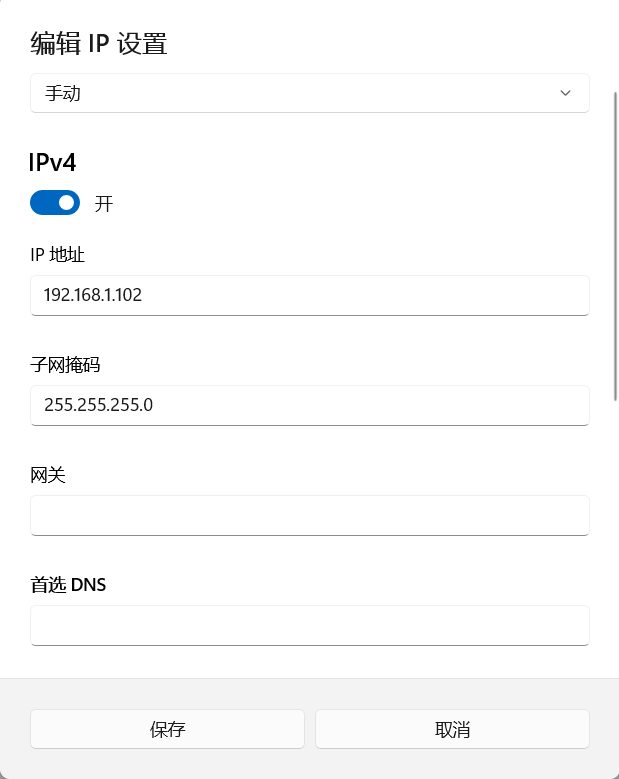
- 如果机械臂的IP为192.168.10.18,则将电脑的IP设置为10网段(参照上面设置)。
- 如果机械臂IP为192.168.1.18 ,则将电脑 ip地址设为1网段。
- 标定板放置在平面上,相机固定在机械臂末端,相机对准标定板。
- 标定过程中,标定板是固定放置在机械臂工作区内的,这个固定位置需要保证安装在机械臂末端的相机能从不同的视角观测到它,标定板的确切位置不重要,因为不必知道其相对于机械臂基座的位姿。但是标定板在标定期间应保持固定,不得移动。
- 运行脚本
collect_data.py,出现一个弹窗。 - 拖动机械臂末端,使呈现相机视野下的标定板清晰、完整、将光标放在弹窗上。
注意:
使出现在相机视野里的标定板和相机镜面呈现一定角度。

下面的拍照姿势不对:

- 点击键盘
s采集数据。 - 移动15-20次机械臂,重复步骤(5)(6),采集不同机械臂姿态下的标定板图片15-20张左右。
注意:
移动机械臂末端旋转轴,每次旋转的角度尽量的大(大于30°)。确保在三个轴(X、Y、Z)上都有足够的旋转角度变化。(可以先绕着机械臂末端z轴旋转多个角度拍摄多副图片,然后绕着x轴旋转)。

计算标定结果
运行脚本compute_in_hand.py,获取标定结果。
得出相机坐标系相对于机械臂末端坐标系的旋转矩阵和平移向量。
眼在手外
采集数据
- 相机连接线连接电脑和D435相机,网线连接电脑和机械臂。
- 电脑的ip和机械臂设置为同一网段。
- 如果机械臂IP为192.168.1.18 ,则将电脑 ip地址设为1网段。
- 如果机械臂的IP为192.168.10.18,则将电脑的IP设置为10网段。
- 将标定板(打印纸质较小的板子,方便固定)固定在机械臂末端,相机固定不动,移动机械臂末端,使标定板出现在相机视野里。
- 标定过程中,标定板安装在机械臂末端执行器上并随机械臂移动。可以直接固定在工具法兰上或由夹具固定安装,安装的确切位置不重要,因为不必知道标定板和末端执行器的相对位姿。重要的是标定板在运动过程中不会出现相对于工具法兰或夹具的位移,它必须被良好地固定住或被夹具紧紧地抓住。建议使用由刚性材料制成的安装支架。
- 运行脚本
collect_data.py,出现一个弹窗。 - 拖动机械臂末端,使呈现相机视野下的标定板清晰、完整、将光标放在弹窗上。
- 点击键盘“s”采集数据。
- 移动15-20次机械臂,重复步骤(5)(6),采集不同机械臂姿态下的标定板图片15-20张左右。
- 移动机械臂末端旋转轴,每次旋转的角度尽量的大(大于30°)
- 确保在三个轴(X、Y、Z)上都有足够的旋转角度变化。
计算标定结果
运行脚本compute_to_hand.py,获取标定结果。
得出相机坐标系相对于机械臂基坐标系的旋转矩阵和平移向量。
误差范围
受采集到的图片的质量影响,标定结果中的平移向量与实际的差距在1cm之内。
标定过程中可能出现的问题
问题1
在计算采集到的数据时。
即执行下面脚本时:
python compute_in_hand.py或
python compute_to_hand.py可能出现下面问题
问题描述:[ERROR:0@1.418] global calibration_handeye.cpp:335 calibrateHandEyeTsai Hand-eye calibration failed! Not enough informative motions--include larger rotations.
问题原因: 采集的图片旋转量不足,特别是缺少足够大的旋转运动。
手眼标定需要机器人在空间中执行一系列运动,以获取相机相对于机器人末端的精确关系。若机器人的运动数据中缺乏足够的旋转变化,尤其是在各个轴向上的显著旋转,标定算法就无法准确计算出手眼关系。
解决方案:
- 增加旋转运动:
- 在数据采集过程中,让机器人执行更大的旋转运动。确保在三个轴(X、Y、Z)上都有足够的旋转角度变化。
- 例如,旋转角度最好能超过30度,这样能提供丰富的运动信息。
- 多样化运动姿态:
- 采集数据时,保证机器人末端执行多样化的姿态变化,包括平移和旋转。
- 避免只在小范围内运动或只在某一轴上运动。
- 增加数据采集次数:
- 采集更多的样本数据,一般来说,至少需要10组以上不同的姿态数据。
- 更多的数据能提高标定的稳定性和准确性。
问题2
问题描述: 运行数据采集程序(python collect_data.py ),总是出现异常(崩溃)而挂掉。
问题原因: 当前程序API版本和机械臂控制器版本不一致。
解决方案:
- 打开示教器,查看当前机械臂控制器版本。
- 示教器:配置-机械臂配置-版本信息。

当前使用机械臂API版本(4.3.3)。
- 如需查看机械臂控制器版本与API版本对应关系,请查看版本变更说明。
根据控制器版本和API版本对应关系,选择特定版本的控制器软件或者API进行升级替换。
- 升级控制器版本方法web版示教器使用说明
手眼标定结果如何使用
机械臂如何捡取物品?
眼在手上
理论
从一个不涉及相机的机械臂开始。它的两个主要坐标系是:
- 机械臂基坐标系
- 末端执行器坐标系
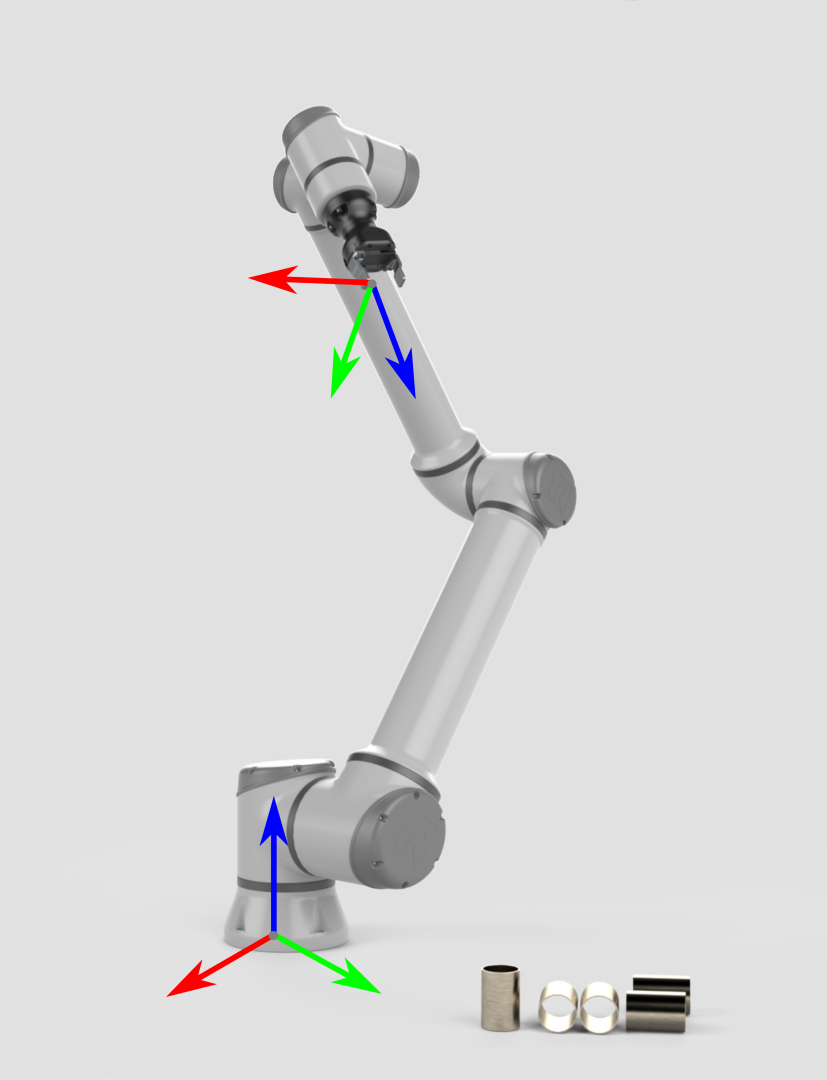
为了捡取物品,机械臂需要知道物品相对于机械臂基坐标系的位姿。通过这些信息以及机器人相关的几何知识,即可算出末端执行器/夹具朝物体移动的关节角度。
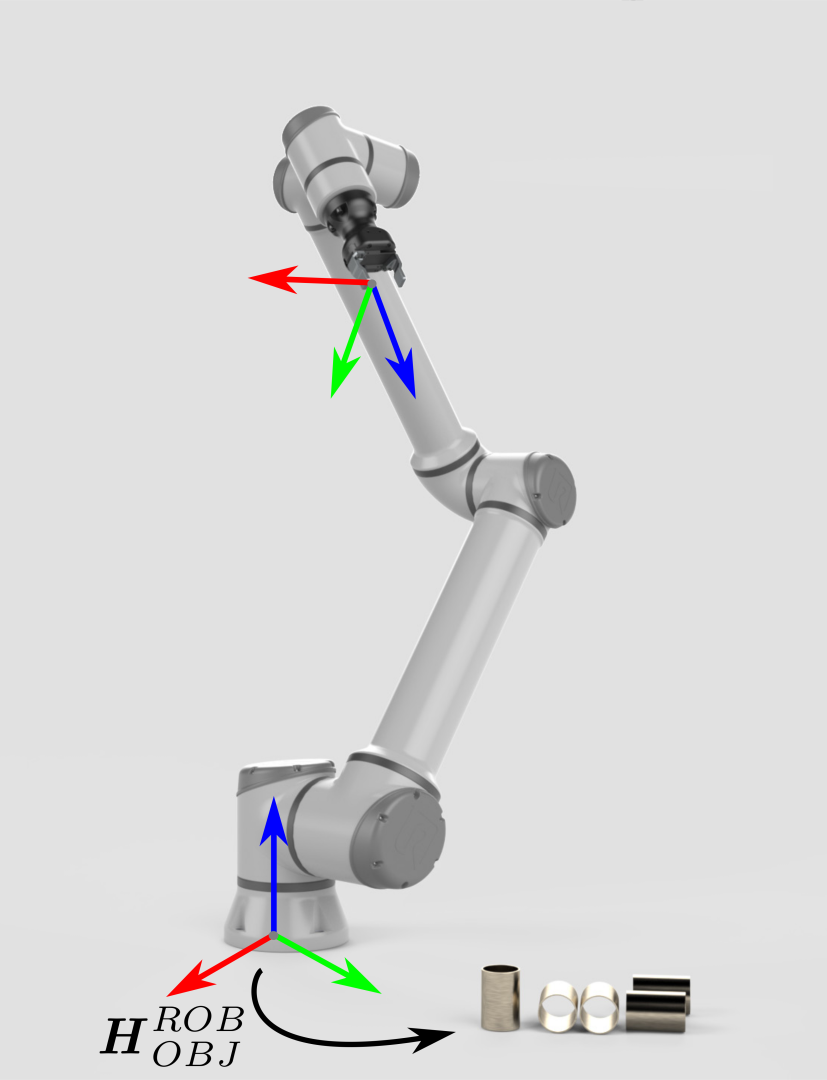
物体相对相机坐标系的位姿可以通过模型识别得到,为了使机械臂能够拾取物体,需要将物体的位姿从相机的坐标系转换到机械臂的基坐标系。
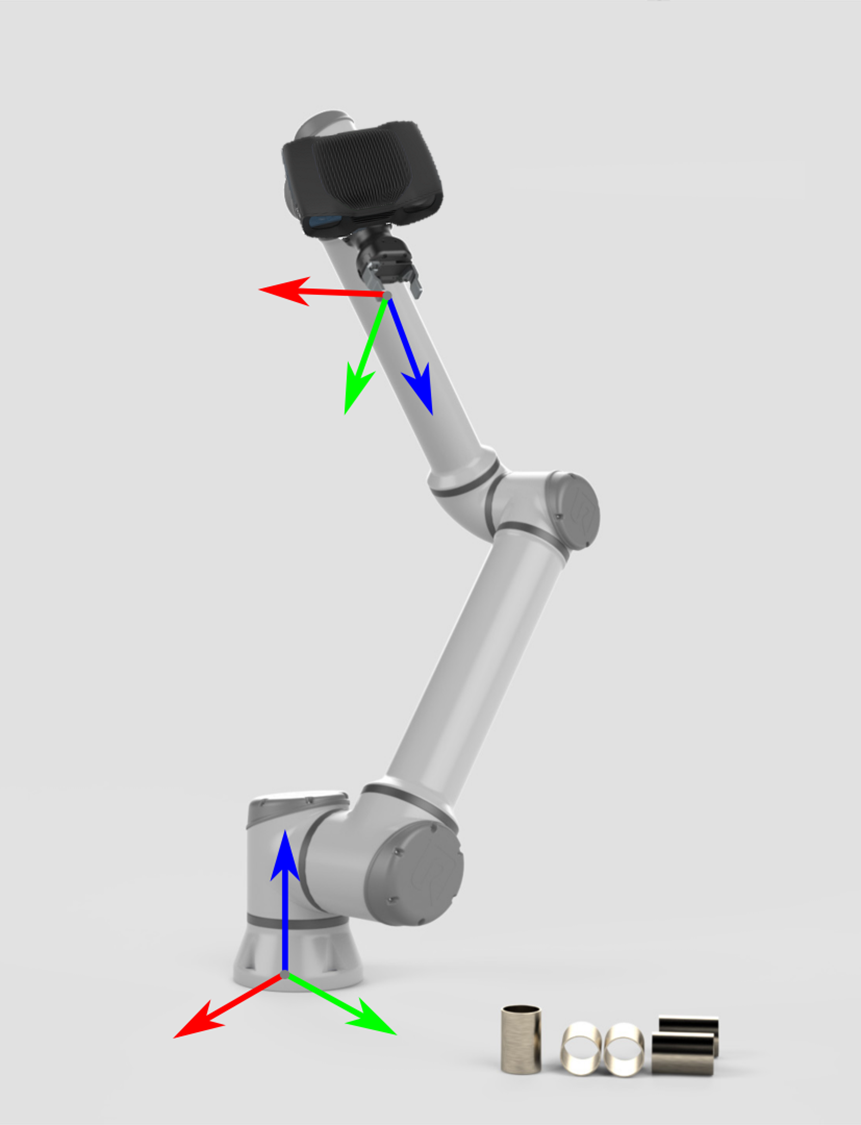
在这种情况下,坐标转换是间接完成的:
末端执行器相对于机械臂基座的位姿
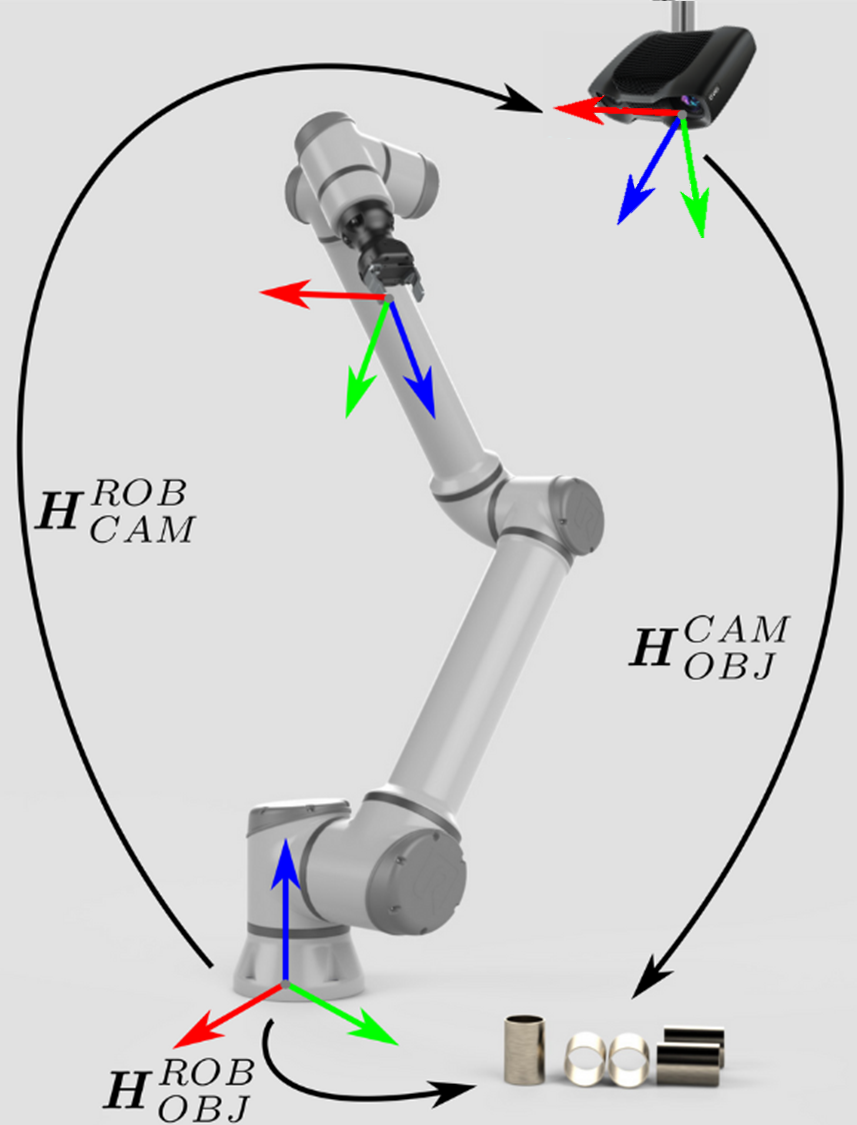
假如物体在相机坐标系是一个3D点或者一个位姿,那么下面说明物体位置作为一个3D点或者一个位姿从相机坐标系转换到机械臂基坐标系的数学理论。

机械臂的位姿用齐次变换矩阵表示。
以下方程描述了如何将单个3D点从相机坐标系转换到机械臂基坐标系:
如果要将物体位姿从相机坐标系转换到机械臂基坐标系。
由此产生的位姿是机械臂当前工具坐标系圆心应该达到的位姿进行捡取。(标定时采集的机械臂位姿也是当前工具坐标系相对于机械臂基坐标系位姿)。
代码
物体在相机坐标系是一个3D点(x,y,z)。
pythonimport numpy as np from scipy.spatial.transform import Rotation as R # 相机坐标系到机械臂末端坐标系的旋转矩阵和平移向量(手眼标定得到) rotation_matrix = np.array([[-0.00235395 , 0.99988123 ,-0.01523124], [-0.99998543, -0.00227965, 0.0048937], [0.00485839, 0.01524254, 0.99987202]]) translation_vector = np.array([-0.09321419, 0.03625434, 0.02420657]) def convert(x ,y ,z ,x1 ,y1 ,z1 ,rx ,ry ,rz): """ 我们需要将手眼标定得到旋转向量和平移向量转换为齐次变换矩阵,然后使用深度相机识别到的物体坐标(x, y, z)和 机械臂末端的位姿(x1,y1,z1,rx,ry,rz)来计算物体相对于机械臂基座的位姿(x, y, z) """ # 深度相机识别物体返回的坐标 obj_camera_coordinates = np.array([x, y, z]) # 机械臂末端的位姿,单位为弧度 end_effector_pose = np.array([x1, y1, z1, rx, ry, rz]) # 将旋转矩阵和平移向量转换为齐次变换矩阵 T_camera_to_end_effector = np.eye(4) T_camera_to_end_effector[:3, :3] = rotation_matrix T_camera_to_end_effector[:3, 3] = translation_vector # 机械臂末端的位姿转换为齐次变换矩阵 position = end_effector_pose[:3] orientation = R.from_euler('xyz', end_effector_pose[3:], degrees=False).as_matrix() T_base_to_end_effector = np.eye(4) T_base_to_end_effector[:3, :3] = orientation T_base_to_end_effector[:3, 3] = position # 计算物体相对于机械臂基座的位姿 obj_camera_coordinates_homo = np.append(obj_camera_coordinates, [1]) # 将物体坐标转换为齐次坐标 obj_end_effector_coordinates_homo = T_camera_to_end_effector.dot(obj_camera_coordinates_homo) obj_base_coordinates_homo = T_base_to_end_effector.dot(obj_end_effector_coordinates_homo) obj_base_coordinates = list(obj_base_coordinates_homo[:3]) # 从齐次坐标中提取物体的x, y, z坐标 return obj_base_coordinates物体在相机坐标系是一个位姿。
pythonimport numpy as np from scipy.spatial.transform import Rotation as R # 相机坐标系到机械臂末端坐标系的旋转矩阵和平移向量(手眼标定得到) rotation_matrix = np.array([[-0.00235395 , 0.99988123 ,-0.01523124], [-0.99998543, -0.00227965, 0.0048937], [0.00485839, 0.01524254, 0.99987202]]) translation_vector = np.array([-0.09321419, 0.03625434, 0.02420657]) def decompose_transform(matrix): """ 将矩阵转化为位姿 """ translation = matrix[:3, 3] rotation = matrix[:3, :3] # Convert rotation matrix to euler angles (rx, ry, rz) sy = np.sqrt(rotation[0, 0] * rotation[0, 0] + rotation[1, 0] * rotation[1, 0]) singular = sy < 1e-6 if not singular: rx = np.arctan2(rotation[2, 1], rotation[2, 2]) ry = np.arctan2(-rotation[2, 0], sy) rz = np.arctan2(rotation[1, 0], rotation[0, 0]) else: rx = np.arctan2(-rotation[1, 2], rotation[1, 1]) ry = np.arctan2(-rotation[2, 0], sy) rz = 0 return translation, rx, ry, rz def convert(x,y,z,rx,ry,rz,x1,y1,z1,rx1,ry1,rz1): """ 我们需要将标定得到的旋转向量和平移向量转换为齐次变换矩阵,然后使用机械臂末端的位姿(x, y, z,rx,ry,rz)和 深度相机识别到的物体坐标(x1,y1,z1,rx1,ry1,rz1)来计算物体相对于机械臂基座的位姿 """ # 深度相机识别物体返回的坐标 obj_camera_coordinates = np.array([x1, y1, z1,rx1,ry1,rz1]) # 机械臂末端的位姿,单位为弧度 end_effector_pose = np.array([x, y, z, rx, ry, rz]) # 将旋转矩阵和平移向量转换为齐次变换矩阵 T_camera_to_end_effector = np.eye(4) T_camera_to_end_effector[:3, :3] = rotation_matrix T_camera_to_end_effector[:3, 3] = translation_vector # 机械臂末端的位姿转换为齐次变换矩阵 position = end_effector_pose[:3] orientation = R.from_euler('xyz', end_effector_pose[3:], degrees=False).as_matrix() T_end_to_base_effector = np.eye(4) T_end_to_base_effector[:3, :3] = orientation T_end_to_base_effector[:3, 3] = position # 计算物体相对于机械臂基座的位姿 # 物体相对于相机的位姿转换为齐次变换矩阵 position2 = obj_camera_coordinates[:3] orientation2 = R.from_euler('xyz', obj_camera_coordinates[3:], degrees=False).as_matrix() T_object_to_camera_effector = np.eye(4) T_object_to_camera_effector[:3, :3] = orientation2 T_object_to_camera_effector[:3, 3] = position2 obj_end_effector_coordinates_homo = T_camera_to_end_effector.dot(T_object_to_camera_effector) obj_base_effector = T_end_to_base_effector.dot(obj_end_effector_coordinates_homo) result = decompose_transform(obj_base_effector) return result
代码中rotation_matrix和translation_vector变量分别是眼在手上手眼标定得到的旋转矩阵和平移向量。
眼在手外
理论
相机可以通过模型获取物体在相机坐标系的里的位姿,物体相对于机械臂的位姿通过相机相对于机械臂基坐标系的位姿和物体相对于相机相机坐标系的位姿通过后乘法计算得到的:

假如物体位置是一个3D点或者一个位姿,那么下面说明物体位置作为一个3D点或者一个位姿从相机坐标系转换到机械臂基坐标系的数学理论。
以下方程描述了如何将单个3D点从相机坐标系转换到机械臂基坐标系:
如果要将物体位姿从相机坐标系转换到机械臂基坐标系。
代码
物体在相机坐标系是一个3D点(x,y,z)。
pythonimport numpy as np # 相机坐标系到机械臂基坐标系的旋转矩阵和平移向量(手眼标定得到) rotation_matrix = np.array([[-0.00235395 , 0.99988123 ,-0.01523124], [-0.99998543, -0.00227965, 0.0048937], [0.00485839, 0.01524254, 0.99987202]]) translation_vector = np.array([-0.09321419, 0.03625434, 0.02420657]) def convert(x ,y ,z): """ 我们需要将旋转向量和平移向量转换为齐次变换矩阵,然后使用深度相机识别到的物体坐标(x, y, z)和 标定好的 相机到基座的 齐次变换矩阵 来计算物体相对于机械臂基座的位姿(x, y, z) """ # 深度相机识别物体返回的坐标 obj_camera_coordinates = np.array([x, y, z]) # 将旋转矩阵和平移向量转换为齐次变换矩阵 T_camera_to_base_effector = np.eye(4) T_camera_to_base_effector[:3, :3] = rotation_matrix T_camera_to_base_effector[:3, 3] = translation_vector # 计算物体相对于机械臂基座的位姿 obj_camera_coordinates_homo = np.append(obj_camera_coordinates, [1]) # 将物体坐标转换为齐次坐标 obj_base_effector_coordinates_homo = T_camera_to_base_effector.dot(obj_camera_coordinates_homo) obj_base_coordinates = obj_base_effector_coordinates_homo[:3] # 从齐次坐标中提取物体的x, y, z坐标 # 组合结果 return list(obj_base_coordinates)物体在相机坐标系是一个位姿。
pythonimport numpy as np from scipy.spatial.transform import Rotation as R # 相机坐标系到机械臂基坐标系的旋转矩阵和平移向量(手眼标定得到) rotation_matrix = np.array([[-0.00235395 , 0.99988123 ,-0.01523124], [-0.99998543, -0.00227965, 0.0048937], [0.00485839, 0.01524254, 0.99987202]]) translation_vector = np.array([-0.09321419, 0.03625434, 0.02420657]) def decompose_transform(matrix): """ 将矩阵转化为位姿 """ translation = matrix[:3, 3] rotation = matrix[:3, :3] # Convert rotation matrix to euler angles (rx, ry, rz) sy = np.sqrt(rotation[0, 0] * rotation[0, 0] + rotation[1, 0] * rotation[1, 0]) singular = sy < 1e-6 if not singular: rx = np.arctan2(rotation[2, 1], rotation[2, 2]) ry = np.arctan2(-rotation[2, 0], sy) rz = np.arctan2(rotation[1, 0], rotation[0, 0]) else: rx = np.arctan2(-rotation[1, 2], rotation[1, 1]) ry = np.arctan2(-rotation[2, 0], sy) rz = 0 return translation, rx, ry, rz def convert(x ,y ,z,rx,ry,rz): """ 我们需要将旋转向量和平移向量转换为齐次变换矩阵,然后使用深度相机识别到的物体位姿(x, y, z,rx,ry,rz)和 标定好的 相机到基座的 齐次变换矩阵 来计算物体相对于机械臂基座的位姿(x, y, z,rx,ry,rz) """ # 深度相机识别物体返回的坐标 obj_camera_coordinates = np.array([x, y, z,rx,ry,rz]) # 将旋转矩阵和平移向量转换为齐次变换矩阵 T_camera_to_base_effector = np.eye(4) T_camera_to_base_effector[:3, :3] = rotation_matrix T_camera_to_base_effector[:3, 3] = translation_vector # 计算物体相对于机械臂基座的位姿 # 物体相对于相机的位姿转换为齐次变换矩阵 position2 = obj_camera_coordinates[:3] orientation2 = R.from_euler('xyz', obj_camera_coordinates[3:], degrees=False).as_matrix() T_object_to_camera_effector = np.eye(4) T_object_to_camera_effector[:3, :3] = orientation2 T_object_to_camera_effector[:3, 3] = position2 obj_base_effector = T_camera_to_base_effector.dot(T_object_to_camera_effector) result = decompose_transform(obj_base_effector) # 组合结果 return result
代码中rotation_matrix和translation_vector变量分别是眼在手外手眼标定得到的旋转矩阵和平移向量。

